Probabilidad en ciencia de los datos

Si alguna vez abriste una hoja de cálculo lleno de números y sentiste que estabas frente a un acertijo sin solución, no eres el único. Hace unos años, Marta (una analista de datos autodidacta) pensó que la probabilidad solo existía para los matemáticos. Hasta que tuvo que decidir si una campaña publicitaria era ‘suerte’ o ‘tendencia’. La diferencia entre ganar o perder estaba –obviamente– en entender la probabilidad. Así descubrimos que, detrás de todo gran análisis de datos, se esconde una lógica de azar… que en realidad es pura ciencia.

Probabilidad sin miedo: rompiendo mitos y confusiones

Hablar de conceptos de probabilidad suele generar cierta incomodidad. Muchos piensan en la probabilidad como algo lejano, reservado para matemáticos o, en el mejor de los casos, para quienes lanzan monedas al aire. Sin embargo, la teoría de probabilidad es mucho más que eso: es el corazón del análisis de datos y la ciencia de datos moderna. Pero, ¿por qué existe tanta confusión en probabilidad?

Errores comunes: ¿Solo lanzar monedas?

Uno de los errores más frecuentes es reducir la probabilidad a ejemplos simples como tirar una moneda o sacar una carta de una baraja. Si bien estos ejemplos ayudan a ilustrar los conceptos básicos, la realidad es que la probabilidad está presente en casi todos los aspectos de la vida y el trabajo. Desde predecir si lloverá mañana, hasta calcular el riesgo de una inversión, la probabilidad es la herramienta que nos permite tomar decisiones informadas bajo incertidumbre.

¿Por qué genera tanto rechazo? El caso de Marta y el miedo a las fórmulas

Imagina a Marta, una profesional brillante, pero que siempre ha sentido rechazo hacia la probabilidad. El simple hecho de ver una fórmula la hace retroceder. No está sola: muchas personas comparten este temor. La raíz suele estar en experiencias pasadas, donde la probabilidad se enseñó como una serie de reglas abstractas, sin conexión con la vida real.

Matt Dancho, experto en ciencia de datos, lo resume así:

‘Entender la probabilidad transforma la manera en que interpretamos los datos.’ – Matt Dancho

Superar el miedo a la probabilidad es clave para abrir la puerta a mejores análisis y a una toma de decisiones más sólida.

Probabilidad en la vida diaria: de la lotería al pronóstico del tiempo

La teoría de probabilidad no solo vive en los libros de texto. Está en la lotería, en los pronósticos del tiempo, en los seguros, e incluso en los algoritmos que filtran el spam en tu correo electrónico. Cada vez que decides si llevar paraguas o no, estás haciendo un análisis de probabilidad, aunque no lo llames así.

En ciencia de datos, la probabilidad es aún más esencial. Research shows que entender conceptos como variables aleatorias, independencia y eventos conjuntos o disjuntos es fundamental para analizar datos y predecir comportamientos. Por ejemplo, los modelos de predicción de clientes o los sistemas de recomendación se basan en estos principios.

Confundir casualidad con causalidad: un error costoso

Uno de los grandes peligros en el análisis de datos es confundir casualidad con causalidad. No es raro encontrar patrones en los datos y asumir que uno causa al otro, cuando en realidad solo están relacionados por azar. Aquí la probabilidad nos ayuda a distinguir entre una simple coincidencia y una relación significativa.

Además, research shows que muchos profesionales creen que la probabilidad es innecesaria, hasta que enfrentan problemas reales de incertidumbre. En ese momento, la falta de conocimientos básicos limita su capacidad de análisis y toma de decisiones.

Eventos conjuntos y disjuntos: la raíz de muchas confusiones

Una de las fuentes clásicas de confusión en probabilidad es no diferenciar entre eventos conjuntos y disjuntos. Por ejemplo, calcular la probabilidad de que ocurran dos eventos a la vez (conjuntos) no es lo mismo que calcular la probabilidad de que ocurra uno u otro (disjuntos). Entender esta diferencia es esencial para evitar errores en el análisis de datos y en la interpretación de resultados.

En resumen, la probabilidad está lejos de ser solo un juego de azar. Es una herramienta poderosa que, bien entendida, permite enfrentar la incertidumbre y tomar mejores decisiones en la vida y en la ciencia de datos.

De la moneda al algoritmo: núcleo de los conceptos clave

Hablar de ciencia de datos sin mencionar los conceptos de probabilidad es como intentar construir una casa sin cimientos. Desde lanzar una moneda hasta programar un algoritmo, la probabilidad es el hilo conductor que une el azar con la toma de decisiones informadas. Matt Dancho, referente en el área, lo resume así:

“En ciencia de datos, las simulaciones son nuestro laboratorio virtual: la probabilidad es el idioma que hablamos.” – Matt Dancho

Pero, ¿qué significa realmente esto? Para entenderlo, es necesario desmenuzar algunos de los conceptos de probabilidad más importantes: variables aleatorias, valores esperados, independencia y simulaciones Monte Carlo. Estos términos pueden sonar intimidantes, pero en realidad, son herramientas cotidianas para quienes trabajan con datos.

Variables aleatorias: el azar hecho número

Las variables aleatorias no son solo nombres técnicos. Son la forma en que los científicos de datos traducen el azar en números. Por ejemplo, al lanzar una moneda, el resultado (cara o cruz) es una variable aleatoria. En ciencia de datos, estas variables permiten modelar fenómenos inciertos, desde el clima hasta el comportamiento de los clientes.

Imagina que quieres predecir cuántos clientes comprarán un producto en una tienda online. No puedes saberlo con certeza, pero puedes asignar probabilidades a cada posible resultado. Así, las variables aleatorias se convierten en la base para analizar y entender la incertidumbre.

El valor esperado: prediciendo el futuro con matemáticas

El valor esperado es otro de los conceptos de probabilidad esenciales. Es, en pocas palabras, el promedio ponderado de todos los resultados posibles de una variable aleatoria. Los casinos lo usan para asegurarse de que, a largo plazo, siempre ganan. Pero no solo sirve para juegos de azar: empresas y analistas lo utilizan para tomar decisiones bajo incertidumbre.

Por ejemplo, si una campaña de marketing tiene un 10% de éxito y genera $100 por venta, el valor esperado por intento es $10. Esto ayuda a decidir si la inversión vale la pena. En ciencia de datos, calcular valores esperados permite comparar estrategias y elegir la más rentable o menos riesgosa.

Independencia: dejando atrás supersticiones

La independencia es un concepto clave para evitar errores comunes. Muchas veces, las personas creen que si una moneda ha salido cara varias veces, es más probable que salga cruz la próxima vez. Pero si los eventos son independientes, el pasado no afecta al futuro.

En ciencia de datos, reconocer la independencia estadística es vital para construir modelos precisos. Si dos variables son independientes, conocer el valor de una no da información sobre la otra. Esto permite simplificar cálculos y evitar conclusiones erróneas.

Simulaciones Monte Carlo: experimentando sin riesgos

Las simulaciones Monte Carlo llevan los conceptos de probabilidad a la acción. Consisten en realizar miles (o millones) de experimentos virtuales para estimar la probabilidad de distintos resultados. Esta técnica es fundamental en sectores como finanzas, logística y análisis de riesgos.

Por ejemplo, para calcular el riesgo de una inversión, se pueden simular miles de escenarios posibles, variando factores como precios, tasas de interés o demanda. Así, se obtiene una visión más realista de lo que podría ocurrir, sin necesidad de esperar años para ver los resultados reales.

En resumen, variables aleatorias, valores esperados e simulaciones Monte Carlo son mucho más que teoría: son la base sobre la que se construyen los algoritmos modernos. Sin estos conceptos de probabilidad, la ciencia de datos no podría ofrecer predicciones ni soluciones prácticas a problemas reales.

Aplicaciones reales: de clientes predecibles a correos (no tan) spam

La probabilidad en ciencia de datos no es solo una teoría abstracta; es el motor que impulsa muchas de las aplicaciones más sorprendentes y útiles del data science moderno. Desde anticipar el comportamiento de los clientes hasta filtrar correos no deseados, las aplicaciones de probabilidad están presentes en casi todas las decisiones inteligentes basadas en datos.

Predicción del comportamiento del cliente: ¿mito o práctica habitual?

¿Es realmente posible predecir lo que hará un cliente? En la práctica, la respuesta es sí, aunque nunca con certeza absoluta. Las empresas de ecommerce y los bancos, por ejemplo, utilizan modelos probabilísticos para analizar patrones de compra, abandono de carrito o incluso la probabilidad de impago. Estos modelos se basan en datos históricos y en técnicas como la regresión logística, el análisis de cohortes y, por supuesto, el Teorema de Bayes.

Research shows que la probabilidad permite transformar grandes volúmenes de datos en predicciones accionables. Por ejemplo, si un cliente ha comprado productos similares en el pasado, el modelo asigna una probabilidad alta de que vuelva a hacerlo. Así, las recomendaciones personalizadas dejan de ser un simple “quizás” y se convierten en una estrategia basada en evidencia.

Detección de fraude y spam: donde la probabilidad deja de ser opcional

En el mundo financiero y digital, la detección de fraude y spam es una de las aplicaciones de probabilidad más conocidas. Aquí, la probabilidad no es solo útil, sino esencial. Los sistemas de detección de spam, por ejemplo, utilizan el Teorema de Bayes para calcular la probabilidad de que un correo sea spam en función de palabras clave, remitentes y patrones de comportamiento.

De manera similar, los bancos aplican modelos probabilísticos para identificar transacciones sospechosas. Si una operación se desvía del comportamiento habitual del usuario, el sistema asigna una probabilidad de fraude y puede activar alertas automáticas. Estos modelos aprenden y mejoran con el tiempo, ajustando sus parámetros a medida que se recopilan más datos.

La lotería de los datos: minoristas que apuestan por lo imprevisible

No todos los patrones son fáciles de predecir. A veces, los datos parecen una lotería. Sin embargo, incluso en la aparente aleatoriedad, la probabilidad en ciencia de datos puede revelar oportunidades. Un caso real: un minorista analizó los tickets de compra y descubrió que ciertos productos, aunque no parecían relacionados, solían comprarse juntos en días específicos. Ajustando promociones y stock a estos patrones “imprevisibles”, logró aumentar sus ventas significativamente.

Este ejemplo ilustra cómo pequeñas mejoras en los modelos probabilísticos pueden tener un impacto comercial enorme. Como bien señala Matt Dancho:

‘Una pequeña variable puede reescribir todo el guion de un análisis.’ – Matt Dancho

El efecto mariposa y los pequeños detalles probabilísticos

En data science, un cambio mínimo en los datos de entrada puede alterar por completo el resultado de un modelo. Esto se conoce como el “efecto mariposa” en probabilidad. Un solo clic, una compra inesperada o un correo abierto pueden cambiar la predicción de un sistema. Por eso, los expertos insisten en la importancia de revisar y ajustar constantemente los modelos probabilísticos.

En resumen, las aplicaciones de probabilidad en ciencia de datos permiten anticipar tendencias, detectar amenazas y personalizar experiencias. No se trata solo de números, sino de comprender y aprovechar la incertidumbre para tomar mejores decisiones.

Lo que no suele enseñarse: probabilidad condicional y el poder del Teorema de Bayes

En el mundo de la ciencia de datos, la probabilidad es mucho más que una simple fórmula matemática. Sin embargo, hay conceptos que rara vez se explican a fondo, como la probabilidad condicional y el Teorema de Bayes. Estos elementos, aunque suenen avanzados o abstractos, son el corazón de muchos algoritmos probabilísticos que usamos a diario, incluso sin darnos cuenta.

¿Por qué tan pocos entienden la probabilidad condicional (y por qué importa tanto)?

La probabilidad condicional suele ser una de las partes más confusas para quienes se inician en la probabilidad en ciencia de datos. ¿Por qué? Porque implica pensar en probabilidades que cambian a medida que recibimos nueva información. No es solo calcular la posibilidad de que ocurra un evento, sino cómo esa posibilidad se ajusta si ya sabemos que ha ocurrido otra cosa.

Por ejemplo, si alguien ya ha visto la primera temporada de una serie, ¿cuál es la probabilidad de que vea la segunda? Esa es una pregunta de probabilidad condicional. Muchos subestiman su utilidad por considerarla demasiado teórica, pero en realidad, es una herramienta poderosa para tomar mejores decisiones, tanto en la vida diaria como en el análisis de datos.

Teorema de Bayes: de herramienta matemática a arma secreta de Google y Netflix

El Teorema de Bayes es una extensión natural de la probabilidad condicional. Permite actualizar nuestras creencias a medida que recibimos nueva información. En palabras de Matt Dancho:

‘El Teorema de Bayes es el comodín que conecta los datos con la intuición.’

Este teorema es el pilar de muchos sistemas modernos. Por ejemplo, los algoritmos probabilísticos detrás de los filtros de spam en tu correo electrónico o las recomendaciones personalizadas en plataformas como Google y Netflix se basan en el Teorema de Bayes. Cada vez que eliges una película o serie, el sistema ajusta sus recomendaciones usando probabilidades condicionadas por tus elecciones previas.

Ejemplo mental: decidir qué serie ver basándonos en probabilidades condicionadas por nuestras elecciones previas

Imagina que has visto varias series de ciencia ficción en Netflix. El sistema, usando probabilidad condicional, calcula que es más probable que te interese otra serie del mismo género. Si de repente ves una comedia romántica, el algoritmo ajusta sus recomendaciones: ahora la probabilidad de que te gusten comedias románticas aumenta. Este proceso de actualización es el Teorema de Bayes en acción.

Este mecanismo es tan sutil que rara vez lo notamos, pero determina gran parte de nuestra experiencia digital. Las grandes tecnológicas aplican estos principios de forma imperceptible, pero determinante, para personalizar contenidos y mejorar la experiencia del usuario.

Pequeñas dosis de probabilidad condicional pueden mejorar tus decisiones cotidianas

No hace falta ser científico de datos para aprovechar la probabilidad condicional en la vida diaria. Por ejemplo, si sabes que suele llover cuando el cielo está nublado, puedes ajustar tus planes en función de esa información. Lo mismo ocurre al tomar decisiones de compra, elegir rutas de viaje o incluso al analizar riesgos en inversiones.

La clave está en entender que cada nueva información puede y debe ajustar nuestras probabilidades. Como muestran los estudios y tutoriales sobre probabilidad en ciencia de datos, dominar estas técnicas ayuda a analizar eventos condicionales y tomar decisiones más informadas.

En resumen, aunque la probabilidad condicional y el Teorema de Bayes pueden parecer complejos, su impacto es tangible en la tecnología y en la vida cotidiana. Aprender a pensar en términos de probabilidades condicionadas transforma la manera en que interpretamos el mundo y tomamos decisiones, tanto grandes como pequeñas.

Recursos inesperados y consejos poco convencionales para dominar la probabilidad

1. Distribuciones estadísticas:

Existen cientos de distribuciones entre las que elegir a la hora de modelar datos. Las opciones parecen infinitas. Utiliza esto como una guía para simplificar la elección.

2. Distribuciones discretas:

Las distribuciones discretas se utilizan cuando los datos solo pueden tomar valores específicos y distintos. Estos valores suelen ser enteros, como el número de llamadas de ventas realizadas o el número de clientes que se han convertido.

3. Distribuciones continuas:

Se usan para datos que pueden tomar cualquier valor dentro de un rango o intervalo. Estos valores suelen ser números reales, como el porcentaje de visitantes que se convierten o los ingresos previstos durante los próximos 6 meses.

4. Función de masa de probabilidad (discretas):

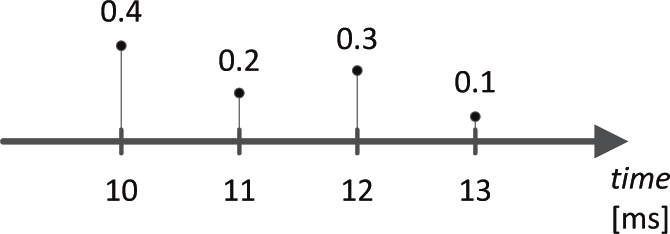
Las distribuciones discretas se describen mediante una función de masa de probabilidad, que indica la probabilidad de que una variable aleatoria discreta sea exactamente igual a un determinado valor. En un gráfico, una distribución discreta suele representarse como una serie de barras, donde cada barra muestra la probabilidad de cada resultado discreto.

5. Función de densidad de probabilidad (continuas):

Las distribuciones continuas se describen mediante una función de densidad de probabilidad. La probabilidad de que la variable tome un valor dentro de un rango concreto se representa como el área bajo la curva de la función dentro de ese intervalo. En un gráfico, una distribución continua se representa normalmente con una curva suave.

6. Modelos paramétricos: muchos modelos asumen una distribución específica.

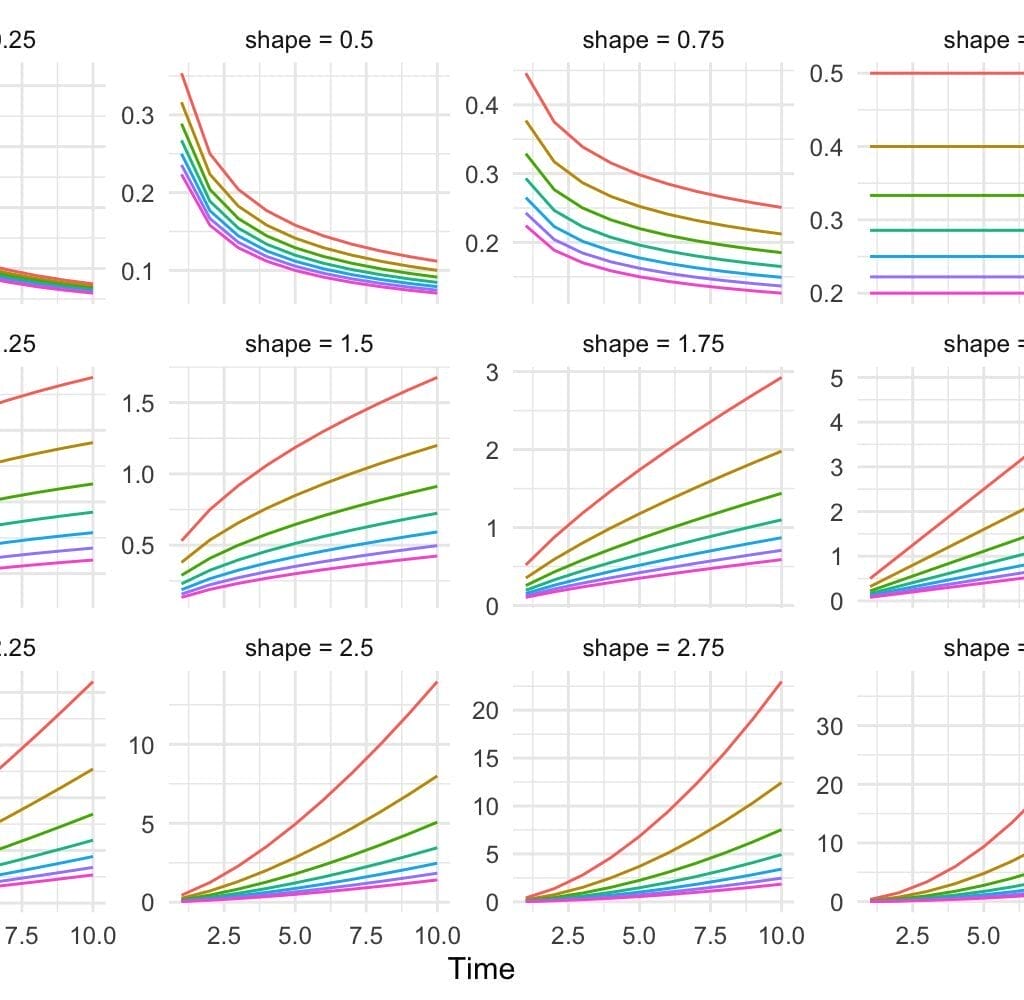
• Regresión lineal: asume que los errores siguen una distribución normal.
• Regresión logística: asume que la variable de respuesta sigue una distribución binomial.

7. Modelos no paramétricos:

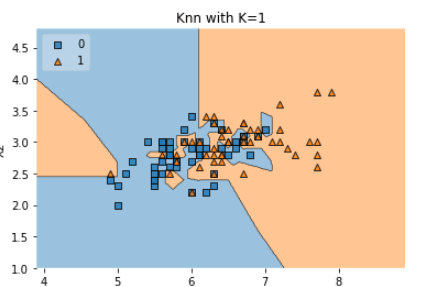
Estos modelos no hacen suposiciones estrictas sobre la forma de la distribución de los datos.

• Árboles de decisión
• K-Vecinos más cercanos (K-NN)
• Máquinas de vectores de soporte (SVM)

8. Funciones de pérdida:

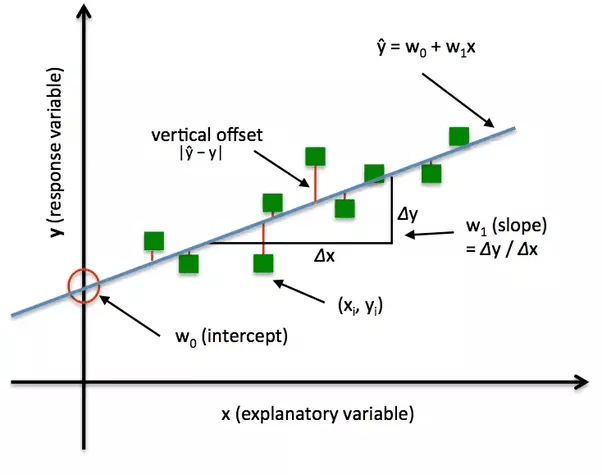
Las distribuciones también aparecen en las funciones de pérdida del aprendizaje automático (por ejemplo, XGBoost, LightGBM, CatBoost). Elegir la función de pérdida adecuada puede mejorar significativamente el rendimiento.

Ejemplos:

• Poisson se utiliza para datos de recuento.
• Tweedie para datos continuos con muchos ceros, como en problemas de previsión de demanda intermitente.

Cuando se habla de probabilidad en ciencia de datos, la mayoría imagina largas fórmulas, libros densos y cursos universitarios. Sin embargo, la realidad es mucho más rica y, a menudo, sorprendente. Dominar la probabilidad teoría no solo depende de memorizar conceptos, sino de experimentar, equivocarse y aprender de la práctica. Como bien señala Matt Dancho, “El mejor profesor de probabilidad es el error, siempre que sepas aprender de él”.

Uno de los recursos inesperados más efectivos para comprender la probabilidad son los juegos de azar y los experimentos caseros. ¿Por qué? Porque el casino, con su mezcla de azar y estrategia, es un laboratorio perfecto para poner en práctica la teoría. Lanzar una moneda, tirar dados o incluso jugar a la ruleta permite observar en tiempo real conceptos como la independencia de eventos, la ley de los grandes números y la distribución de probabilidades. Estos ejemplos cotidianos hacen que la teoría cobre vida y se fije en la memoria mucho más rápido que cualquier explicación abstracta.

No obstante, no todos tienen acceso a un casino ni tiempo para organizar experimentos cada día. Aquí es donde los tutoriales breves en video se convierten en aliados fundamentales. Plataformas como YouTube ofrecen playlists especializadas, como esta serie de probabilidad para ciencia de datos, que desmenuzan los conceptos más complejos en pocos minutos. Estos videos no solo ayudan a despejar el aburrimiento, sino que también permiten repasar la teoría a ritmo propio, pausando y repitiendo según la necesidad.

Ahora bien, uno de los consejos menos convencionales pero más valiosos es practicar el “error controlado”. Equivocarse a propósito, en un entorno seguro, es una metodología de aprendizaje poderosa y subestimada. Por ejemplo, al simular experimentos donde se espera un resultado y se obtiene otro, se pueden identificar los puntos débiles en la comprensión de la probabilidad teoría. Este enfoque, lejos de ser un fracaso, es una oportunidad para fortalecer el razonamiento y evitar errores en escenarios reales de ciencia de datos.

Además, en la era digital, las comunidades online se han convertido en un recurso salvavidas. Foros y grupos de analistas comparten casos reales, discuten problemas prácticos y ofrecen soluciones que rara vez aparecen en los libros de texto. Participar en estos espacios permite acceder a una variedad de perspectivas y aprender de la experiencia colectiva. Según estudios recientes, la colaboración en comunidades mejora significativamente la capacidad para resolver problemas complejos y aplicar la probabilidad en contextos reales.

Por supuesto, los cursos de probabilidad siguen siendo un pilar fundamental. Opciones como el curso de probabilidad para ciencia de datos de Harvard ofrecen una base sólida y actualizada, combinando teoría y práctica. Estos recursos, junto con los tutoriales y la interacción comunitaria, forman un ecosistema de aprendizaje que va mucho más allá del aula tradicional.

En conclusión, aprender probabilidad es una aventura que trasciende los límites del aula. Los juegos, los errores controlados, los videos cortos y las comunidades online son probabilidad recursos tan valiosos como cualquier libro de texto. La clave está en atreverse a experimentar, preguntar y, sobre todo, aprender de cada paso, incluso de los que parecen un tropiezo. Porque, como bien dice Matt Dancho, el error es el mejor maestro cuando se sabe escuchar.